1. 主成分分析
优点:降低数据的复杂性,识别最重要的多个特征。
缺点:不一定需要,且可能损失有用信息。
使用数据类型:数值型数据
2. 在NumPy中实现PCA
将数据转换成前K个主成分的伪码:
去除平均值(让样本矩阵中心化,即每一个维度减去该维度的均值,使每一维度上的均值为0)
计算协方差矩阵
计算协方差矩阵的特征值和特征向量
将特征值从大到小排序
保留最上面的K个特征向量
将数据转换到上述K个特征向量构建的新空间中
补充阅读:协方差矩阵
(1)一个维度上方差的定义:
(2)协方差的定义:
方差是协方差的一个特例,X与其自身的协方差就是X的方差。
分母为n-1是因为随机变量的数学期望未知,以样本均值代替,自由度减一。
协方差就是定义了两个维度之间的相关性,即这个样本的两个维度之间有没有关系。
协方差为0,证明这两个维度之间没有关系;协方差为正,两个维度正相关;协方差为负,两个维度负相关。
(3)协方差矩阵:
对n个维度,任意两个维度都计算一个协方差,组成矩阵。
直观地,对于一个含有x,y,z三个维度的样本,协方差矩阵如下:
可以看出,对角线表示了样本在各个维度上的方差,其他元素表示不同维度两两之间的相关性。
例:
假设原始数据为5个样本,每个样本有2个特征x和y。矩阵是:
第一步,样本矩阵中心化(计算每个维度的均值,所有样本都减去均值)
维度x的均值为2,维度y的均值为1。
各维度去均值后,矩阵是:
这时,两个维度上的均值都为0。
第二步,计算协方差矩阵
协方差矩阵:
第三步,计算协方差矩阵的特征值和特征向量
特征值2.5对应的特征向量是eigenVectors的第1列:
特征值0.5对应的特征向量是eigenVectors的第2列:
第四步,将特征值按照从大到小的顺序排列,选择其中最大的k个,然后将其对应的k个特征向量分别作为列向量组成特征向量矩阵
这里特征值只有2个,我们选取最大的那个2.5,对应的特征向量是:
第五步,将样本点投影到选取的特征向量上。
假设样本数为m,特征数为n,减去均值后的样本矩阵为DataAdjust(m×n),协方差矩阵为C(n×n),选取的k个特征向量组成的矩阵为TopEigenVectors(n×k),那么投影后的低维数据LowDimData为:
这里是
这样就将原始样本的n维(这个例子n=2)特征变成了k维(这个例子k=1),这k维就是原始特征在k维上的投影。
第六步,查看重构之后的数据,用于调试(假设K取值为n,重构回去的数据reconMat应该与原始数据Data重合)
程序清单 PCA算法
from numpy import *
import matplotlib
import matplotlib.pyplot as plt
def loadDataSet(fileName, delim='\t'):
fr = open(fileName)
stringArr = [line.strip().split(delim) for line in fr.readlines()]
datArr = [list(map(float,line)) for line in stringArr]
# python3 needs list()
return mat(datArr)
def pca(dataMat, topNfeat=9999999):
meanVals = mean(dataMat, axis=0)
dataAdjust = dataMat - meanVals #remove mean
covMat = cov(dataAdjust, rowvar=0)
eigVals,eigVects = linalg.eig(mat(covMat))
eigValInd = argsort(eigVals) #sort, sort goes smallest to largest
eigValInd = eigValInd[:-(topNfeat+1):-1] #cut off unwanted dimensions
topEigVects = eigVects[:,eigValInd] #reorganize eig vects largest to smallest
lowDimDataMat = dataAdjust * topEigVects#transform data into new dimensions
reconMat = (lowDimDataMat * topEigVects.T) + meanVals
return lowDimDataMat, reconMat
dataMat = loadDataSet('testSet.txt')
lowDimDataMat, reconMat = pca(dataMat, 1)
fig = plt.figure()
ax = fig.add_subplot(111)
ax.scatter(dataMat[:,0].flatten().A[0], dataMat[:,1].flatten().A[0], marker='^', s=90)
ax.scatter(reconMat[:,0].flatten().A[0], reconMat[:,1].flatten().A[0], marker='o', s=50, c='red')
plt.show()
运行结果如图1: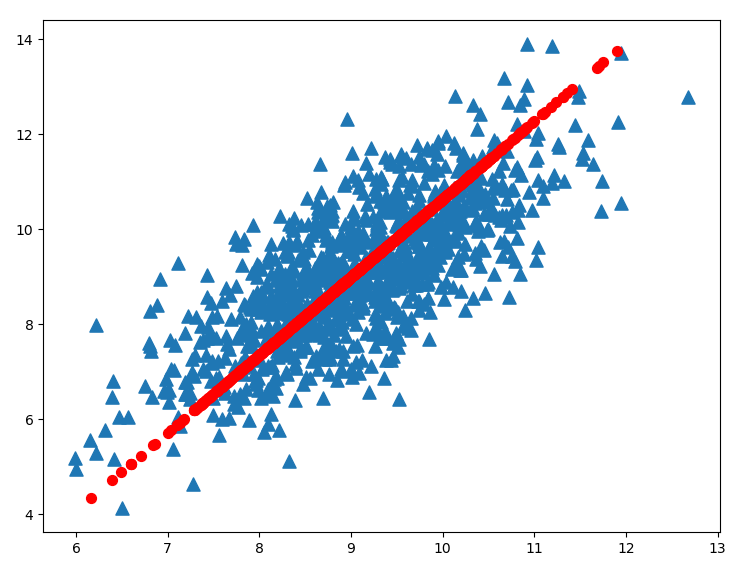
用到的数据集testSet.txt
参考文献:
[1] (美) Harrington Peter著. 机器学习实战[M]. 李锐, 李鹏, 曲亚东, 王斌, 译. 北京: 人民邮电出版社, 2013.
